Number of Arithmetic Triplet (Leetcode)
2024-01-12
- Algorithm
- JavaScript
- LeetCode
문제
You are given a 0-indexed, strictly increasing integer array nums and a positive integer diff. A triplet (i, j, k) is an arithmetic triplet if the following conditions are met:
i < j < k,nums[j] - nums[i] == diff, andnums[k] - nums[j] == diff.
Return the number of unique arithmetic triplets.
Example 1:
Input: nums = [0,1,4,6,7,10], diff = 3
Output: 2
Explanation: (1, 2, 4) is an arithmetic triplet because both 7 - 4 == 3 and 4 - 1 == 3. (2, 4, 5) is an arithmetic triplet because both 10 - 7 == 3 and 7 - 4 == 3.
Example 2:
Input: nums = [4,5,6,7,8,9], diff = 2
Output: 2
Explanation: (0, 2, 4) is an arithmetic triplet because both 8 - 6 == 2 and 6 - 4 == 2. (1, 3, 5) is an arithmetic triplet because both 9 - 7 == 2 and 7 - 5 == 2.
Constraints:
- 3 <= nums.length <= 200
- 0 <= nums[i] <= 200
- 1 <= diff <= 50
numsis strictly increasing.
접근
diff에 맞춰 배열 안의 숫자 세 개만 규칙에 맞추면 되니 그대로 구현해볼까라고 생각했다.
외부에 temp 라는 별도 변수를 두고, 첫 번째 규칙을 찾기 위해 루프 안에 nums[i]+diff 를 넣고
결과값을 indexOf 메소드를 사용하여 인덱스를 temp 에 저장 후에 또 nums[temp]+diff 가 존재 한다면 규칙의 갯수를 찾는 것이니 리턴해야하는 result++ 를 해주면 된다고 생각했다.
정답 (맞음)
/**
* @param {number[]} nums
* @param {number} diff
* @return {number}
*/
var arithmeticTriplets = function(nums, diff) {
var temp;
var result = 0;
for(let i=0; i<nums.length; i++){
if(!nums.includes(nums[i]+diff)) continue
else {
temp = nums.indexOf(nums[i]+diff);
if(!nums.includes(nums[temp]+diff)) continue
else result++
}
}
return result;
};
규칙이 없으면 빠르게 다음 index로 넘어가도록 하였다.
최고의 방법?
현재 구현은 배열의 각 요소에 대해 includes 메서드를 사용하여 등차수열을 이루는 다음 두 숫자가 존재하는지 확인하고 있습니다. 이 접근법은 간단하지만, includes와 indexOf 메서드 모두 배열을 순회하는 작업을 수행하므로, 각각 \(O(n)\)의 시간 복잡도를 가지고, 전체 함수는 이보다 더 큰 시간 복잡도를 가질 것입니다.
최적화를 위해 다음과 같은 접근법을 사용할 수 있습니다:
-
HashSet 사용: 각 숫자의 존재 여부를
\(O(1)\)시간에 확인할 수 있는Set을 사용합니다. -
단일 순회: 배열을 한 번만 순회하면서 각 숫자에 대해
num + diff와num + 2*diff가Set에 존재하는지 확인합니다.
이 접근법을 사용하면 함수의 시간 복잡도를 \(O(n)\)으로 줄일 수 있습니다.
다음은 최적화된 함수의 구현 예시입니다:
var arithmeticTriplets = function(nums, diff) {
let numSet = new Set(nums);
let result = 0;
for (let num of nums) {
if (numSet.has(num + diff) && numSet.has(num + 2 * diff)) {
result++;
}
}
return result;
};
이 코드에서는 numSet을 사용하여 각 숫자의 존재 여부를 빠르게 확인하고, 배열을 한 번만 순회하여 필요한 모든 조건을 검사합니다. 이렇게 하면 불필요한 중복 순회를 피하고 성능을 향상시킬 수 있습니다.
내 접근법 vs 최적화 접근법 차이
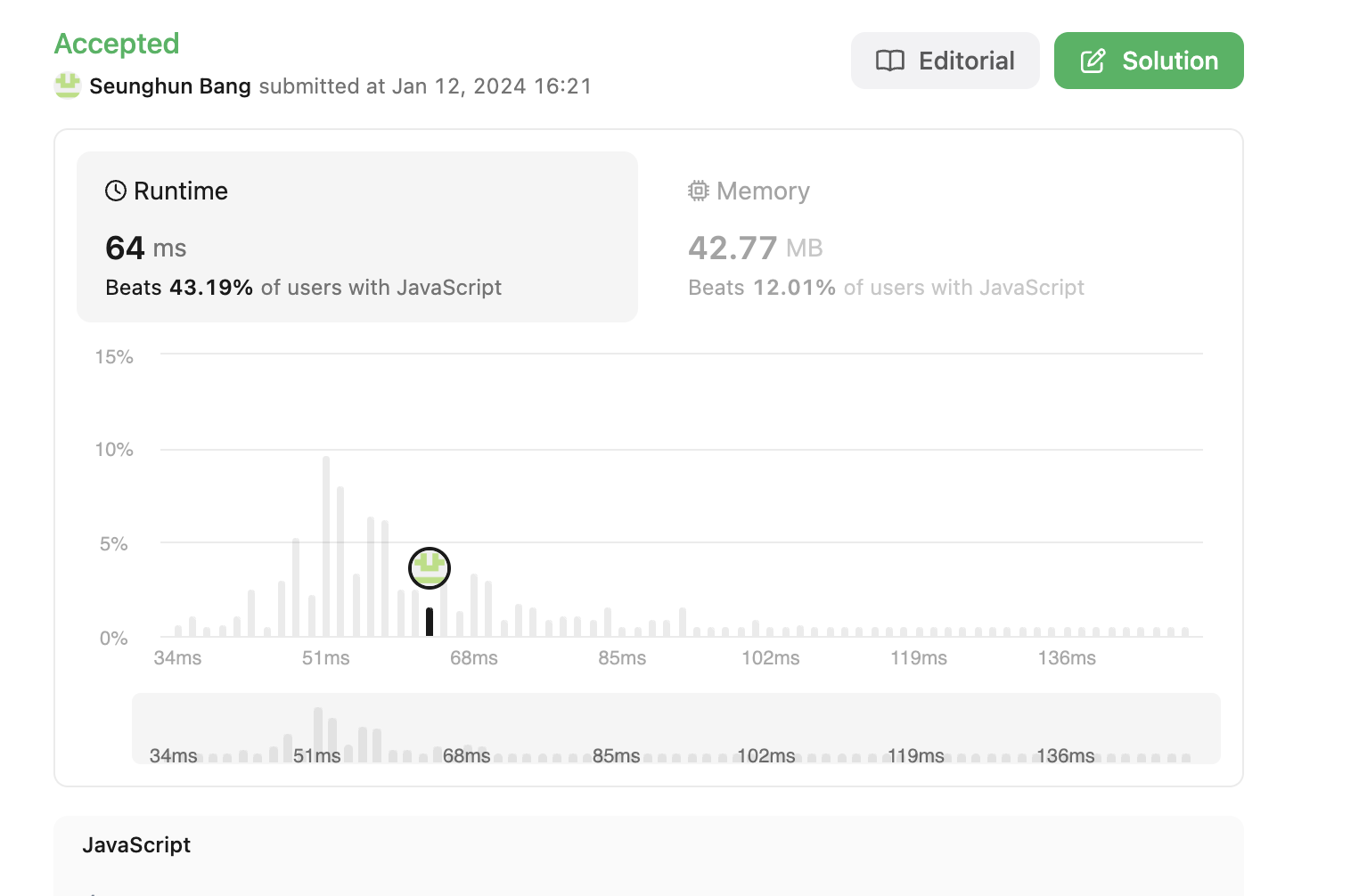
내 접근법
-
중첩된 배열 탐색: 각 요소에 대해
includes를두 번 사용하여 배열 내 다른 요소의 존재 여부를 확인합니다. -
시간 복잡도: 각
includes호출은\(O(n)\)의 시간 복잡도를 가지므로, 전체 함수의 시간 복잡도는 대략\(O(n^3)\)가 됩니다. -
반복된 탐색 작업: 동일한 값을 여러 번 탐색하여 중복 작업이 발생할 수 있습니다.
-
효율성 문제: 큰 배열에 대해 비효율적이며, 실행 시간이 길어질 수 있습니다.
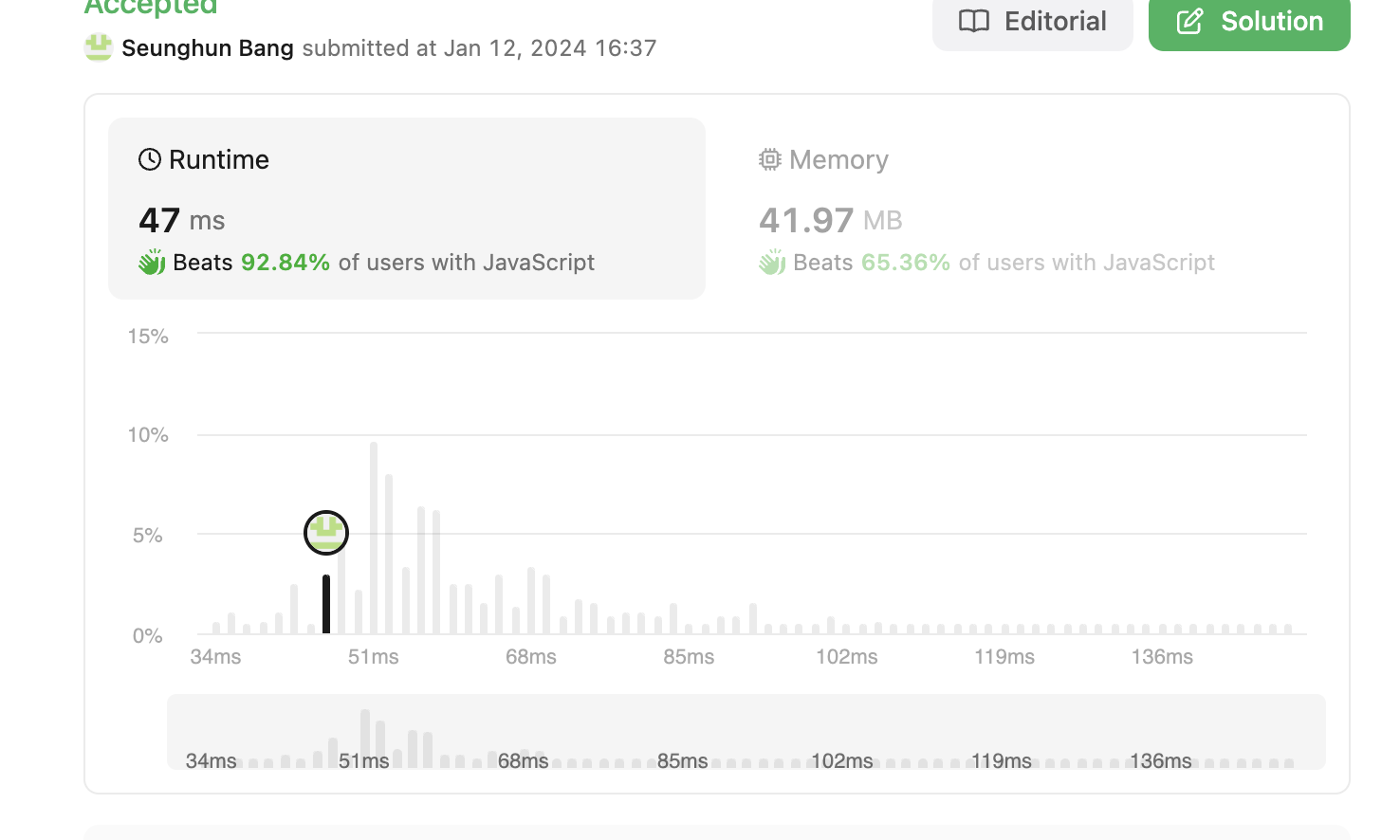
최적화된 접근법
-
HashSet 사용:
Set을 사용하여 각 요소의 존재 여부를\(O(1)\)시간에 빠르게 확인합니다. -
단일 순회: 배열을 한 번만 순회하면서 각 숫자에 대해
num + diff와num + 2 * diff가Set에 존재하는지 확인합니다. -
시간 복잡도: 전체 함수의 시간 복잡도는
\(O(n)\)입니다. -
효율성 향상: 큰 배열에서도 효율적으로 작동하며, 반복된 탐색을 피할 수 있습니다.
결론:
최적화된 접근법은 Set을 사용하여 중복되는 탐색을 피하고, 배열을 단 한 번만 순회하여 필요한 조건을 검사합니다. 이 방식은 효율성이 높으며, 특히 큰 데이터 세트에 대해서 성능이 뛰어납니다. 원래의 접근법은 간결하고 직관적이지만, 큰 배열에서는 시간 복잡도가 증가하여 성능 문제가 발생할 수 있습니다.
링크드 리스트란(L...
3 Sum 세 개의...